马尔可夫决策 MDP 基本概念 (一)

本文将简要介绍马尔可夫过程 (Markov Processes) 与马尔可夫奖励过程 (Markov Reward Processes)。

1 前言

最近准备写一个系列，从马尔可夫决策过程(Markov Decision Processes, MDP) 到部分可观测马尔可夫决策过程 (Partially Observable Markov Decision Processes, POMDP), 再到分布式马尔可夫决策过程 (Decentralized Markov Decision Processes, Dec-MDP)。

要了解 MDP ，首先要了解马尔可夫过程 (Markov Processes)和马尔可夫奖励过程 (Markov Reward Processes)，这两者是 MDP 的基础。本文将按如下顺序介绍:

马尔可夫过程 (Markov Processes)
马尔可夫奖励过程 (Markov Reward Processes)
马尔可夫决策过程 (Markov Decision Processes)

2 马尔可夫过程 (Markov Processes)

2.1 马尔可夫性质 (Markov Property)

马尔可夫过程为什么叫这个名字呢，因为它具有马尔可夫性质。马尔可夫性质简而言之，就是未来发生的事情只与当前状态有关而与过去无关，是一个无记忆的过程，它要求状态包含可能对未来产生影响的所有信息。

举例说明，假设每天的天气有三种状态：晴天、阴天、下雨。我们将第 $i$ 天的状态记为 $S_i$ 。若第 7 天下雨，那么有
$$
S_7=下雨
$$
如果我们假设 $S_i$ 仅取决于 $S_{i-1}$ ，即第 $i$ 天的天气仅取决于第 $i-1$ 天的天气，这就满足马尔可夫性，用数学公式来描述就是
$$
\mathbb{P}\left[ S_{t+1}|S_t \right] =\mathbb{P}\left[ S_{t+1}|S_t,S_{t-1},…,S_1 \right]
$$

举例说明，若第 6 天天晴，则第七天有0.2的概率下雨；若第 6 天阴天，则第七天有0.3 的概率下雨；若第 6 天阴天，则第七天有 0.5 的概率下雨；第 7 天下雨的概率只与第 6 天的天气有关，而与前面 5 天的状态无关。

2.2 状态转移矩阵 (State Transition Matrix)

很容易可以看出来，由于只有三种天气，前后两天的天气组合共有 $3\times 3=9$ 种，那么总共就有 9 种天气变化的概率，它们叫作状态转移概率。将这 9 个概率按一定规则写进矩阵，就是状态转移矩阵。

那这个规则是怎样的呢？若我们将天晴、阴天、下雨这三种状态编号为 1、2、3，则状态转移矩阵中的第 $i$ 行，第 $j$ 列的元素意义如下
$$
P_{ij}=\mathbb{P}\left[ S_{t+1}=\text{状态}i|S_t=\text{状态}j \right]
$$
换句话说，就是前一天天气为状态 $i$，后一天天气为状态 $j$ 的概率，按照这样的规则，整个状态转移矩阵 $P$ 为
$$
\begin{matrix}
& \text{to}\newline
P=\text{from}& \left[ \begin{matrix}
P_{11}& P_{12}& P_{13}\newline
P_{21}& P_{22}& P_{23}\newline
P_{31}& P_{32}& P_{33}\newline
\end{matrix} \right]\
\end{matrix}
$$

不难看出，状态转移矩阵 $P$ 每一行的和都为 1，因为概率之和必为 1。

2.3 马尔可夫过程的定义

马尔可夫过程就是具有马尔可夫性的随机过程，上述天气的例子描述了一个满足马尔可夫性、随着时间的推移，天气不断随机变化的过程，这就是一个马尔可夫过程。马尔可夫过程用元组 $<\mathcal{S},\mathcal{P}>$ 描述。

$\mathcal{S}$ 是所有状态的集合，在刚才的例子中 $\mathcal{S}$ 就是三种不同的天气组成的集合
$\mathcal{P}$ 是状态转移矩阵

2.4 例子

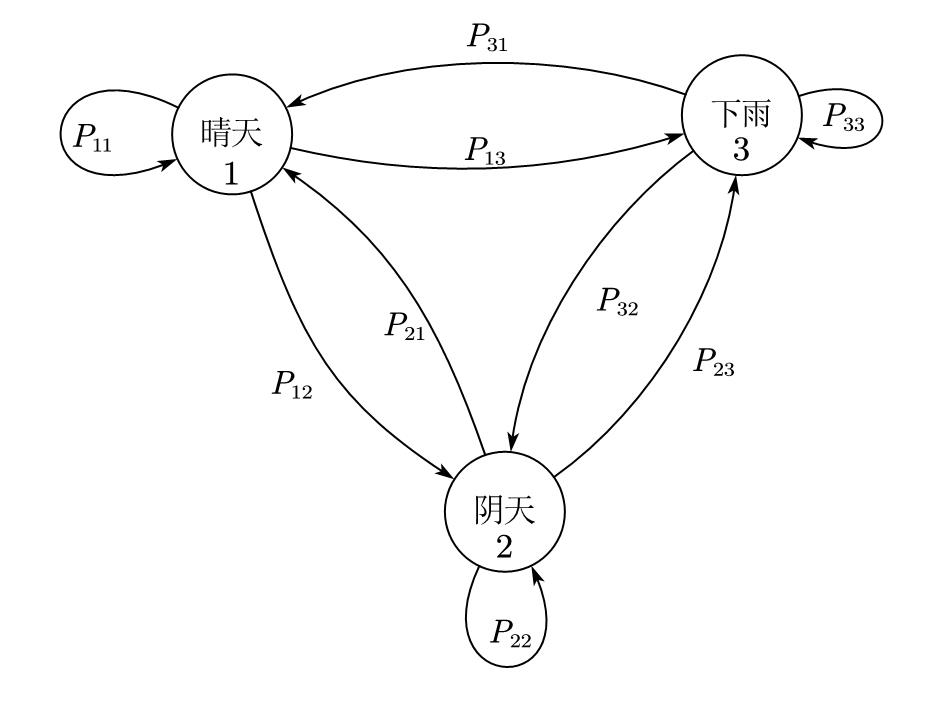
将前面描述天气变化的马尔可夫过程画成图，如下图所示。马尔可夫过程都可以用这样的图来表示。

下面我们看另一个稍微复杂一点的例子，这是一个描述学生学习的马尔可夫过程。在这个例子中，学生共有三节课要学习，在上课过程中，学生有一定概率走神，去刷 Facebook或睡觉，也有可能去酒吧，还有可能坚持把三堂课学完，最终通过考试，按照同样的方法画成图，如下图所示。

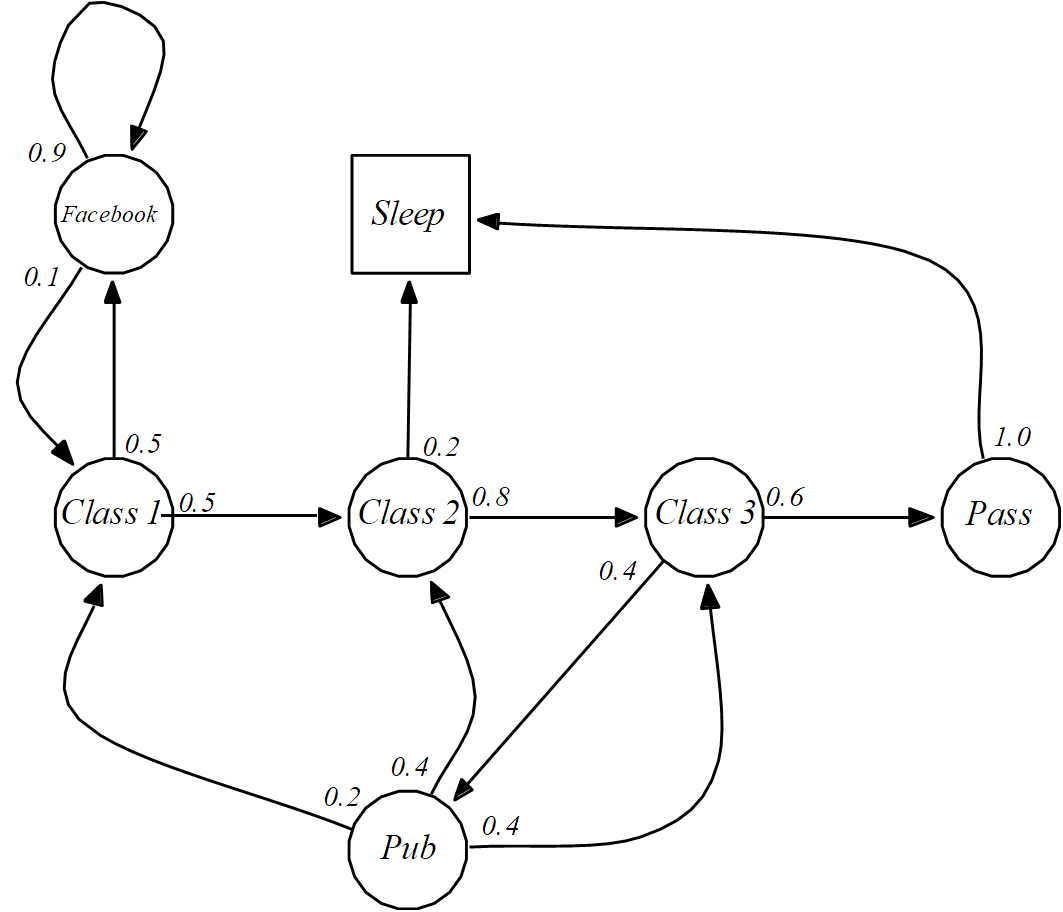
将其状态转移概率写成状态转移矩阵，如该公式所示，可以看到，该矩阵的每行之和都是1。
$$
\mathcal{P}=\begin{matrix}
& \begin{matrix}
\text{C}1& \text{C}2& \text{C}3& \text{Pass}& \text{Pub}& \text{FB}& \text{Sleep}\newline
\end{matrix}\newline
\begin{array}{l}
\text{C}1\newline
\text{C}2\newline
\text{C}3\newline
\text{Pass}\newline
\text{Pub}\newline
\text{FB}\newline
\text{Sleep}\newline
\end{array}& \left[ \begin{matrix}
\ \ \quad & 0.5& \ \ \quad & \ \ \quad & \ \ \quad & 0.5& \ \ \quad \newline
\ \ & \ \ & 0.8& \ \ & \ \ & \ \ \qquad& 0.2\newline
\ \ & \ \ & \ \ & 0.6& 0.4& \ \ & \ \ \newline
\ \ & \ \ & \ \ & \ \ & \ \ & \ \ & 1.0\newline
0.2& 0.4& 0.4& \ \ & \ \ & \ \ & \ \ \newline
0.1& \ \ & \ \ & \ \ & \ \ & 0.9& \ \ \newline
\ \ & \ \ & \ \ & \ \ & \ \ & \ \ & 1.0\newline
\end{matrix} \right]\
\end{matrix}
$$
与刚才天气的例子不同，这个马尔可夫过程有一个终止状态，一旦进入这个状态，整个过程就结束了，这个状态通常可能是游戏结束的状态。为了与其他普通状态一起表示，这个终止状态可以视为以概率 1 转移到自身，这样做的目的是方便处理。

3 马尔可夫奖励过程

有奖励的马尔可夫过程就是马尔可夫奖励过程，为什么需要有奖励呢？

马尔可夫过程仅仅对环境的变化进行了定义，而我们的最终目的通常是为了让智能体 (agent) 能够在环境中学习出好的策略，智能体怎么学习呢，靠的是奖励。若对我们有利，就给正奖励；若对我们不利，就给负奖励。

3.1 定义

马尔可夫奖励过程是带奖励的马尔可夫过程，马尔可夫过程用元组 $<\mathcal{S},\mathcal{P},\mathcal{R},\gamma>$ 描述。

$\mathcal{S}$ 是所有状态的集合
$\mathcal{P}$ 是状态转移矩阵
$\mathcal{R}$ 是奖励
$\gamma$ 是折损因子 (discount factor)，$\gamma \in[0,1]$，这个后面解释，是用来选择“短视”或“远视”的。

3.2 例子

上述学生学习的马尔可夫过程加上奖励后，如下图所示

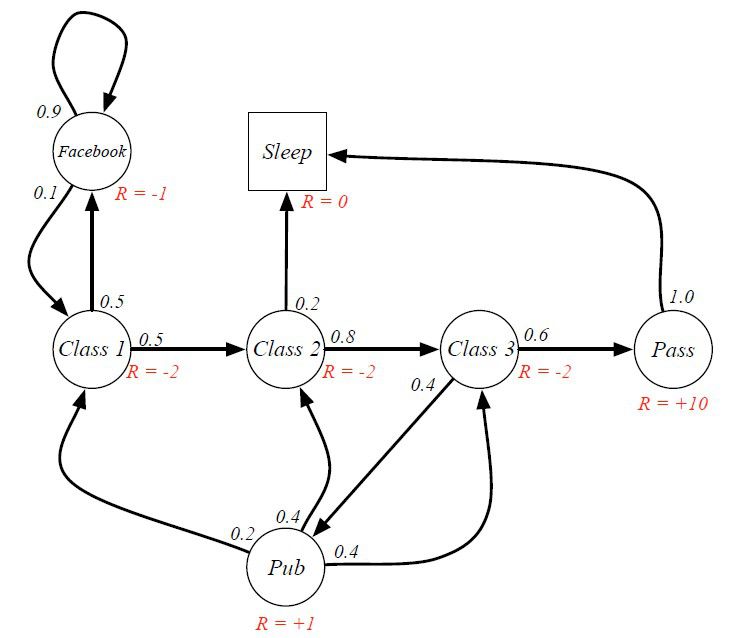
学习的目的是为了通过考试，所以给予正奖励；而学习的过程中比较枯燥、辛苦，给负奖励；临时去酒吧能暂时感到快乐，给较小的正奖励。我们最终的目标是为了取得尽可能高的奖励。

若某学生的学习过程是 C1 C2 C3 Pass Sleep，那么在整个过程中获得的累计奖励是 4；若某学生的学习过程是 C1 FB FB C1 C2 Sleep，那么在整个过程中获得的累计奖励是 -8。

3.3 回报

回报 (return) $G_t$ 定义为从时刻 $t$ 开始，之后获取的所有奖励乘上折损因子再求和，即
$$
G_t=R_{t+1}+\gamma R_{t+2}+…=\sum_{k=0}^{\infty}{\gamma ^kR_{t+k+1}}
$$
由于 $\gamma \in[0,1]$，$\gamma$ 控制着对未来奖励的关心程度。若 $\gamma=0$，$G_t$ 退化为 $G_t=R_{t+1}$ 意味着只考虑当前的奖励，不关心未来的奖励，最短视；相应地，若 $\gamma=1$，意味着最远视。

$\gamma$ 越接近 $0$ 则越短视
$\gamma$ 越接近 $1$ 则越远视

3.4 为什么需要折损因子

大多数 MRP 或 MDP 中都引入了折损因子，这是为什么呢？主要有以下几个方面的原因。

数学处理方便
防止回报 $G_t$ 趋于正无穷
模型与现实存在偏差，越远的未来可能偏差越大
在金融等领域有实际物理意义
与人类和动物的行为类似，人们更喜欢及时奖励

要注意的是回报 $G_t$ 与前面在整个过程中获得的累计奖励 $\sum_{t=0}^{\infty}{R_t}$ 是不同的，回报是站在当前的视角下考虑未来，因此需要乘上 $\gamma$；在整个过程中获得的累计奖励，是结束后再统计获得的奖励，二者的时间节点是不同的。

4 总结

马尔可夫过程就是满足马尔可夫性质的随机过程，为了让智能体在环境中学习，引入了奖励，这就是马尔可夫奖励过程。奖励分为即时奖励和未来奖励，折损因子 $\gamma$ 用于平衡“短视”与“远视”。

5 参考资料

RL Course by David Silver

下一节：未完待续